Table des matières

1 Nombres et calculs
2 Géométrie
- 2.1 Alignement de trois points dans le plan.
- 2.2 Équation de droite passant par deux points donnés.
3 Fonctions
4 Statistique et probabilités

Nombres et calculs¶

Un encadrement de √2 d’amplitude inférieure ou égale à $10^{−n}$ par balayage.¶

On sait que √2 ≈ 1.4142135623730951... ce qui va permettre de vérifier l'algorithme.

def balayage(n):
    """renvoie un couple encadrant √2 avec la précision n"""
    a=1
    b=2
    x=a
    for i in range(1,n+1): # pour i allant de 1 à n
        h=10**(-i)
        x=a
        while x**2<2:
            x=x+h
        a=x-h  # on vient de dépasser √2. On repart de la valeur précédente
    return (round(x-h,n),round(x,n)) # round arrondi avec n chiffres après la virgule

balayage(6)

par la méthode de Héron¶

from fractions import Fraction

def heron(a,n):
    """renvoie le couple de fractions encadrant √a (a>1) après n boucles"""
    x = Fraction(1, 1)  # 1/1 est inférieur à √a
    y = Fraction(a, 1)  # a/1 est supérieur à √a
    for i in range(n):  # pour i allant de 0 inclus à n exclu 
        y = (x+y)/2
        x = a/y
    return('√'+str(a)+' est entre '+str(x)+' et '+str(y))

heron(2,3) # approche √2 en 3 boucles

from math import sqrt
815/577 , 577/408, sqrt(2)

Déterminer si un entier naturel a est multiple d’un entier naturel b.¶

On ne va pas utiliser les opérations de base Python :

% reste de division euclidienne (17 % 3 donne 2)
// quotient de division euclidienne (17 // 3 donne 5)

Version naïve¶

on balaye les multiples de $b$

def a_multiple_de_b(a,b):
    """renvoie True (vrai) si a est un multiple de b, False sinon"""
    m=0 # m est alors le premier multiple de b
    n=0 # n compte la multiplicité de b dans m 
    while m < a:
        m = m + b # on passe au multiple suivant
        n = n + 1 # la multiplicité augmente de 1
    if a == n * b: # ou si a == m 
        return True
    else:
        return False

a_multiple_de_b(569,19)

a_multiple_de_b(570,19)

Version pythonesque :¶

On enlève $b$ de $a$ tant qu'on peut le faire strictement.
On regarde ce qui reste

def a_multiple_de_b(a,b):
    """renvoie True (vrai) si a est un multiple de b, False sinon"""
    while a>b: 
        a -= b    # raccourci pour dire : On enlève b à a
    return a==b   # Le résultat d'un test est booléen !

a_multiple_de_b(569,19)

a_multiple_de_b(570,19)

a et b entiers donnés, déterminer le plus grand multiple de b inférieur ou égal à a.¶

On prend l'algorithme précédent.
On ajoute un compteur.

def combien_b_dans_a(a,b):
    n=0 # compte la multiplicité de b
    while a>=b: # >= car on a besoin de comptabiliser la dernière soustraction lorsque a=b
        a -= b  # enlève b de a (raccourci de a = a - b)  
        n += 1  # ajoute 1 à n (raccourci de n = n + 1)
    return n

combien_b_dans_a(57,7)

combien_b_dans_a(56,7)

combien_b_dans_a(55,7)

Déterminer si un entier naturel est premier.¶

On choisit ici d'utiliser les possibilités de python et donc cette version n'est pas adaptée aux élèves de seconde.
On utilise ici l’opération python n%i qui donne le reste de la division euclidienne de $n$ par $i$.
On utilise la liste "diviseurs" qui contiendra tous les diviseurs de $n$.
- la méthode append permet d’ajouter un élément à une liste,
- la fonction len(liste) renvoie la longueur d'une liste.

def estPremier(n):
    """renvoie True (vrai) si n est premier et False sinon."""
    diviseurs=[]
    for i in range(1,n+1):       # i prend les valeurs entières de 1 à n
        if n%i==0:               # si i divise n
            diviseurs.append(i)  # on l'ajoute à la liste des diviseurs
    return len(diviseurs)==2     # un nombre premier n'a que 2 diviseurs. le résultat du test est le booléen cherché

estPremier(47123)

estPremier(47123456)

On pourra diviser le temps de calcul en arrêtant de chercher les diviseurs supérieurs à √n.

Attention, la liste ne contient plus que la moitié des diviseurs.

%timeit(estPremier(47123456)) # durée d'exécution de la fonction

from math import sqrt

def estPremier_(n):
    """renvoie True (vrai) si n est premier et False sinon."""
    diviseurs=[]
    l=int(sqrt(n))+1
    for i in range(1, l):  # i prend les valeurs entières de 1 à √n
        if n%i==0:               # si i divise n
            diviseurs.append(i)  # on l'ajoute à la liste des diviseurs
    return len(diviseurs)==1     # le résultat du test est le booléen cherché

estPremier_(49)

%timeit(estPremier_(47123456)) # durée d'exécution de la fonction

Déterminer la 1ere puissance d’un nombre positif $b$ supérieure ou inférieure à $a$.¶

par balayage¶

On procède par balayage comme pour le plus grand multiple de $b$ inférieur à $a$.

def combien_puissance_b_dans_a(a,b):
    """renvoie l'exposant de la plus grande puissance de b (b > 1) inférieure ou égale à a"""
    p=1 # m est un multiple de b
    e=0 # e est l'exposant de b dans p 
    while p<a:
        p = p * b
        e = e + 1
    if p == a:
        return e
    else:
        return e-1

combien_puissance_b_dans_a(1000, 3)

combien_puissance_b_dans_a(243,3)

version pythonesque¶

def combien_puissance_b_dans_a(a,b):
    """renvoie l'exposant de la plus grande puissance de b (b > 1) inférieure ou égale à a"""
    n=0 # compte la multiplicité de b
    while a>=b: # >= car on a besoin de comptabiliser la dernière division lorsque a=b
        a /= b  # divise a par b (raccourci de a = a / b)
        n += 1  # ajoute 1 à n (on peut écrire n = n + 1)
    return n

combien_puissance_b_dans_a(1000, 3)

combien_puissance_b_dans_a(243, 3)

Géométrie¶

Alignement de trois points dans le plan.¶

Il est intéressant d'utiliser la notion de tuple. Python comprend

A=(1, -3)

comme un mathématicien, le point A est représenté par ses coordonnées (1 ; -3).

On accède à l'abscisse de A avec A[0] et à son ordonnée avec A[1].

Cela ouvre la possibilité de réponse suivante :

vecteur¶

def vecteur(A,B):
    """renvoie les coordonnées du vecteur AB 
    lorsque A et B sont des points du plan définis par leurs coordonnées"""
    return (B[0]-A[0], B[1]-A[1])

Qu'on peut utiliser ainsi :

A = (2, 3)
B = (-1, 5)
u = vecteur(A,B)
v = vecteur(B, A)
print (u)
print (v)
print ("Avec A", A, "et B", B,", on a le vecteur AB", u)

Colinéarité de vecteurs¶

def colineaire(u, v):
    """renvoie vrai si les vecteurs u et v sont colinéaires
    lorsque u et v sont des vecteurs du plan définis par leurs coordonnées"""
    return u[0]*v[1] == u[1]*v[0]

Qu'on peut utiliser ainsi :

colineaire(u, v)

w = (6, 4)
colineaire (u, w)

On peut définir le déterminant :

def determinant(u, v):
    """renvoie le déterminant des vecteurs u et v 
    lorsque u et v sont des vecteurs du plan définis par leurs coordonnées"""
    return u[0]*v[1] - u[1]*v[0]

Qu'on peut utiliser ainsi :

determinant((1, 3), (4, 11))

Alignement de points¶

Les fonctions précédentes étant construites, la réponse est quasi immédiate :

def alignes(A, B, C):
    """renvoie vrai si les points A, B et C sont colinéaires
    lorsque A, B et C sont des points du plan définis par leurs coordonnées"""
    return colineaire(vecteur(A, B), vecteur(A, C))

Qu'on peut utiliser ainsi :

M = (2, 3)
N = (-1, 5)
P = (5, 1)
alignes(M, N, P)

def affiche_alig(A, B, C):
    """renvoie une chaîne de caractères qui dit si les points a, B et C sont alignés"""
    if alignes(A, B, C):
        return ("les points A" + str(A) + ", B" + str(B) + "et C" + str(C) + "sont alignés")
    else :
        return ("les points A" + str(A) + ", B" + str(B) + "et C" + str(C) + "ne sont pas alignés")

affiche_alig(M, N, P)

Une amélioration pour les plus rapides peut être de définir les points par des triplets ("Nom du point", abscisse, ordonnée)

Une amélioration pour mathématicien peut être de permettre un nombre quelconque de coordonnées.

Équation de droite passant par deux points donnés.¶

On garde l'équivalence point $\equiv$ tuple de 2 éléments.

Voici deux versions du même algorithme :

version 1¶

On garde les notations du cours de collège

def eq_droite(A,B):
    """ renvoie une équation de la droite (AB)
    lorsque A et B sont des points du plan définis par leurs coordonnées"""
    (x_A, y_A) = A  # permet d'utiliser les notations du cours grace à l'affectation multiple de python
    (x_B, y_B) = B
    if x_A == x_B:
        if y_A == y_B:
            droite="Il n'est pas possible de donner UNE équation de droite avec un seul point !"
        else:
            droite="Droite « verticale » d'équation x ="+str(x_A)+"."
    elif y_A == y_B:
        droite = "Droite « horizontale » d'équation y ="+str(y_A)+"."
    else:
        m = (y_B-y_A)/(x_B-x_A)
        p = y_A-m*x_A
        droite = "Droite oblique d'équation y ="+str(m)+"x +"+str(p)+"."
    return droite

eq_droite((2,3),(2,33))

eq_droite((2,3),(2,3))

eq_droite((2,3),(-1,3))

eq_droite((2,3),(-1,-9))

version 2¶

Chaque composante du tuple est une coordonnée.

def eq_droite(A,B):
    """ renvoie une équation de la droite (AB)
    lorsque A et B sont des points du plan définis par leurs coordonnées"""
    if A[0] == B[0]: # sans les notations du cours
        if A[1] == B[1]:
            droite = "Il n'est pas possible de donner UNE équation de droite avec un seul point !"
        else:
            droite = "Droite « verticale » d'équation x ="+str(A[0])+"."
    elif A[1] == B[1]:
        droite = "Droite « horizontale » d'équation y ="+str(A[1])+"."
    else:
        m = (B[1] - A[1])/(B[0]-A[0])
        p = A[1] - m*A[0]
        droite = "Droite oblique d'équation y ="+str(m)+"x +"+str(p)+"."
    return droite # droite est une chaîne de caractères

eq_droite((2,3),(2,33))

eq_droite((2,3),(2,3))

eq_droite((2,3),(-1,3))

eq_droite((2,3),(-1,-9))

Version 3¶

On pourrait décider que la fonction renvoie simplement le tuple $(m, p)$ où $m$ est le coefficient directeur et $p$ l'ordonnée à l'origine de la droite.

L'avantage est alors que le résultat est réutilisable pour créer une fonction par exemple.

On peut aussi envisager :

def eq_cartesienne(A, B):
    """ renvoie a, b et c d'une équation de la droite (AB) sous la forme ax+by+c=0 
    lorsque A et B sont des points du plan définis par leurs coordonnées"""
    if A == B:
        return None  # il n'y a pas une droite passant par un seul point
    else:
        u = vecteur(A, B) # il faut avoir précédemment définie la fonction vecteur
        return(-u[1], u[0], A[0]*u[1]-A[1]*u[0])

eq_cartesienne((2,3),(2,3))

eq_cartesienne((2,3),(2,33))

eq_cartesienne((2,3),(-1,3))

eq_cartesienne((2,3),(-1,-9))

On peut alors écrire une fonction affiche_eq_cart(a, b, c) qui met en forme le résultat de l'appel de la fonction.

On peut également écrire une fonction qui indique si deux droites définies par 4 points sont identiques ou non.

Fonctions¶

Prenons une fonction dont on sait qu’elle est croissante puis décroissante sur un intervalle [a ; b], donc qui admet un maximum sur cet intervalle.

Estimation d'un maximum par balayage¶

def f(x):
    return -3*x**3 + 4*x+1 # On définit ici l'expression de la fonction f

def balayage(f, a, b, n):
    """ renvoie un couple définissant l'intervalle contenant l'antécédent
     du maximum de f avec n chiffres significatifs """
    #n est donc le nombre de chiffres souhaités après la virgule 
    e = 10**(-n)
    #e est l'amplitude de la précision souhaitée
    #a est la Borne inférieure de l'intervalle dans lequel le maximum a été repéré
    #b est la Borne supérieure de l'intervalle dans lequel le maximum a été repéré
    maxi = f(a)  # maxi va évoluer. On initialise le balayage
    while b - a > e:
        amplitude = b-a
        for i in range(11):    #On découpe arbitrairement [a ; b] en 10. i=0 → a. i=10 → b.
            x = a+amplitude/10*i #calcul des abscisses obtenues en divisant [a ; b] en 10
            if f(x) > maxi :
                maxi = f(x)
                x_max = x
        a = x_max-amplitude/10 #On réduit l'intervalle dans lequel on va appliquer
        b = x_max+amplitude/10 #à nouveau le balayage jusqu'à la précision demandée
    return (a, b)

Exemples d'utilisation

balayage(f, 0, 2, 3)

balayage(f, 0, 2, 7)

balayage(f, 0, 2, 10)

On voit qu'il y a un problème de stabilité des calculs à partir de $n=8$.

$\left(10^{-7}\right)^3 =10^{-21}$ est inférieur à l'erreur de représentation de 0,1 par un flottant en double précision avec la norme IEE-754, comme l'indique la documentation de python qui est très bien faite.

Rappel : Pour un écart inférieur à $ ε \approx 2.220446049250313 \times 10^{-16}$ python considère que 2 flottants sont égaux.

Extremum par dichotomie¶

Calculer les images de 3 nombres ne permet pas de localiser l'extremum !

Sur cette illustration, on voit que $f(0)=f(2)=0$ et $f(1)=1$ ne permet pas de savoir où se situe le maximum de $f$.

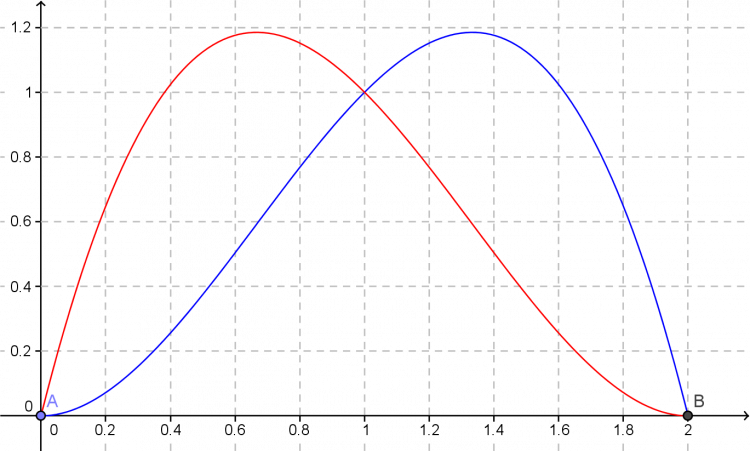
$image geogebra$

On fera donc de la trichotomie !

Je ne le ferai pas avec les élèves.

def trichotomie(f, a, b, n):
    """ renvoie un couple définissant l'intervalle contenant l'antécédent
     du maximum de f avec n chiffres significatifs """
    #n est le nombre de chiffres souhaités après la virgule 
    e = 10**(-n)
    #e est la précision souhaitée
    #a est la Borne inférieure de l'intervalle dans lequel le maximum a été repéré
    #b est la Borne supérieure de l'intervalle dans lequel le maximum a été repéré
    while b-a>e:
        h = (b-a)/3
        c = a + h
        d = b - h
        if f(c)<=f(d):
            a = c
        else:
            b = d
    return (a, b)

trichotomie(f, 0, 2, 7)

trichotomie(f, 0, 2, 8)

trichotomie(f, 0, 2, 10)

On a encore le même problème à partir du même moment ! Cela semble confirmer le problème de stabilité .

On pourrait adapter pour obtenir un minimum.

Approximer la longueur d’une portion de courbe représentative de fonction.¶

on prend une fonction continue sur un intervalle [a ; b] !

On approche la longueur en cumulant celles des n segments dont les abscisses des extrémités vont de $a$ à $b$ par pas de $h=\dfrac{b-a}{n}$ :

On utilise des fonctions préalables.

La fonction :

def f(x):
    return x**2

La norme d'un vecteur :

from math import sqrt, log

def norme(u):
    """Renvoie la norme d'un vecteur à partir de ses coordonnées quelques soient leurs nombres"""
    s = 0 
    for coord in u:      # ce calcul est indépendant de la dimension
        s = s + coord**2
    return sqrt(s)

Distance entre 2 points :

def distance(A, B):
    """Renvoie la distance séparant les points du plan définis par un couple de coordonnées"""
    return norme(vecteur(A, B))

Et la fonction finale

def longueurCourbe(f,a,b,n):
    """Renvoie une approximation de la longueur de la courbe 
    représentant une fonction f sur l'intervalle [a ; b] 
    par la longueur d'un polygone à n côtés"""
    longueur = 0
    M = (a,f(a))  # on se place au point initial
    h = (b-a)/n   # on calcule le pas
    for i in range(n):
        x = M[0] + h
        y = f(x)
        N = (x, y)  # N est le point suivant
        longueur = longueur + distance(M, N)
        M = N     # on repart du nouveau point
    return longueur

longueurCourbe(f, 0, 1, 5)

longueurCourbe(f, 0, 1, 50)

longueurCourbe(f, 0, 1, 100)

(2*sqrt(5) + log (2+sqrt(5))) / 4

Utiliser Python, le tableur ou la calculatrice, pour mettre en évidence l’aspect de programme de calcul.¶

Télépathie¶

On regarde d'abord la vidéo.

Attention, les noms des célébrités ne restent pas longtemps à l'écran.

def programme(n):
    '''renvoie le résultat du programme indiqué par le magicien pour un nombre n de 10 à 99'''
    x = n - n//10 # on enlève le chiffre des dizaines. a//b est le quotient de la division euclidienne de a par b 
    x = x - n%10  # on enlève le chiffre des unités. a%b est le reste de la division euclidienne de a par b 
    return x

On teste tous les nombres !

for n in range(10, 100):
    print(programme(n))

D'un coup, c'est moins magique.

On peut tenter une explication mathématique si la classe s'y prête.

Un autre tour provenant d'Henry Dudeney.¶

« Lancez trois dés, les ranger horizontalement.

Multipliez le premier chiffre (celui de gauche ) par 2,
ajoutez 5 au résultat,
multipliez ce nombre par 5,
lui ajouter alors le second dé
et multipliez le nombre obtenu par dix,
ajoutez enfin le dernier dé. Notez le résultat. »

Je retrouve les valeurs des 3 dés à tous les coups. Et vous ?

Un dernier tour d'un des frères Bogdanoff¶

Autrement dit :

Prenez un nombre entier au hasard connu de vous seul.
Ajoutez-y l'entier suivant.
Demandez à la personne de votre choix, un autre entier au hasard et ajoutez-le au résultat précédent.
Diviser par 2.
Retrancher le nombre initialement choisi.

Le résultat final est ...

Exploiter un logiciel de géométrie dynamique ou de calcul formel, la calculatrice ou Python pour décrire les variations d’une fonction donnée par une formule.¶

Sur ce coup, soit on fait une représentation de la fonction, soit on fait de la merde.

Je n'ai peur ni de l'un ni de l'autre.

Représentation graphique¶

def f(x):
    return x**3-3*x

import matplotlib.pyplot as plt  # import du traitement grahique
import numpy as np      # import d'une bibliothèque efficace
x=np.linspace(-3,3,100) # on coupe l'intervalle de -3 à 3 en 100
plt.plot(x,f(x))  # on place les points avec ses coordonnées
plt.ylabel('polynôme de degré 3')
plt.xlabel("l'axe des abcisses")
plt.show()

Maintenant, la calculatrice, Geogebra, Xcas, ... font ça très bien et Python ne présente pas d'intérêt

De la ...¶

def sens_variation(f, a, b):
    h = (b - a) / 10 # h est le pas de parcours de l'intervalle
    tableau = [] #On crée une liste qui va stocker les résultats
    x1 = a
    for i in range(10):
        x2 = x1 + h
        y1 = f(x1)
        y2 = f(x2)
        if y1 < y2:
            tableau.append("c") # on ajoute à la liste, c ou ↗ pour croissant
        else:
            tableau.append("d") # on ajoute à la liste, d ou ↘ pour décroissant 
        x1 = x2
    return tableau

sens_variation(f, -3, 3)

Cela peut permettre de conjecturer que f est croissante puis décroissante puis croissante sur [-3 ; 3]
On peut affiner la conjecture en modifiant l’algorithme de manière à afficher les abscisses.

Ça restera de la ...

Statistique et probabilités¶

Pour des données réelles ou issues d’une simulation, lire et comprendre une fonction écrite en Python renvoyant la moyenne $m$, l’écart type $s$, et la proportion d’éléments appartenant à $[m-2s, m+2s]$.¶

from math import sqrt # On l'a déjà en mémoire dans jupyter notebook, mais il ne faudra pas l'oublier

def stats(liste):
        n = len(liste)   # On mémorise la taille de la liste
        m = sum(liste)/n # On calcule la moyenne m
        list_ecar_2 = [(x-m)**2 for x in liste] # On crée la liste des carrés des écarts à la moyenne
        variance = sum(list_ecar_2)/n           # On calcule sa moyenne, la variance
        s = sqrt(variance)            # on calcule l'ecart-type statistique
        a = m - 2*s
        b = m + 2*s
        compteur = 0
        for i in range(n):
                if a <= liste[i] <= b : # on peut aussi utiliser "liste[i]<=b and liste[i]>=a"
                        compteur += 1 # on ajoute 1 au compteur
        proportion = compteur/n
        return [m, s, proportion] #On renvoie un tableau qui contient la moyenne, l'écart-type et la proportion d’éléments appartenant à [m-2s,m+2s].

Utilisons cette fonction :

tableau = [i**2 for i in range(100)] # on fabrique la liste des 100 premiers carrés
stats(tableau) # On demande le calcul des statistiques

from random import random
alea = [abs(random()-random()) for i in range(1000)] # on simule 1000 segments aléatoires en coupant l'intervalle [0;1] en 3
stats(alea) # On demande le calcul des statistiques

Lire et comprendre une fonction Python renvoyant le nombre ou la fréquence de succès dans un échantillon de taille $n$ pour une expérience aléatoire à deux issues.¶

On simule un succès avec une probabilité $p$.
On répète $n$ fois et on compte.

from random import random

def succes(p):
    """renvoie True (vrai) avec la probabilité p et False avec la probabilité 1-p"""
    return random()<p  # random() renvoie un nombre aléatoire de [0;1]

def nb_succes(n,p):
    """renvoie le nombre de succès lors de n répétitions, dans des conditions identiques
    et indépendantes, d'une épreuve de Bernoulli"""
    # n est le nombre de répétitions de la simulation
    # p est la probabilité testée
    c = 0 # c est le compteur du nombre de succès
    for k in range(n): # k est le compteur du nombre de répétitions
        if succes(p):
            c = c + 1 # ou c += 1
    return c  # ou c/n pour être en fréquence

nb_succes(1000, 0.5)

Utilisation pour l'estimation d'une proportion¶

va représenter graphiquement 100 simulations d'une taille donnée mais pour une proportion $p$ aléatoire.

On demande à l'élève d'estimer cette proportion connue de python seul.
Python analyse la réponse
On demande à l'élève de diminuer le nombre d'échantillons dès qu'il a 2 réponses successives suffisamment précises.

from random import random        #import la fonction alea depuis la bibliothèque random
import matplotlib.pyplot as plt  # import du traitement grahique pyplot depuis la bibliothèque matplotlib

########    fonctions utiles ############
def succes(p):
    """ fonction qui renvoie True (vrai) avec la probabilité p et False avec la probabilité 1-p"""
    return random()<p  # random() renvoie un nombre aléatoire de [0;1]

def nb_succes(taille, p):
    """renvoie le nombre de succès lors de n répétitions, dans des conditions identiques
    et indépendantes, d'une épreuve de Bernoulli"""
    # n est le nombre de répétitions de la simulation
    # p est la probabilité testée
    c = 0 # c est le compteur du nombre de succès
    for k in range(taille): # k est le compteur du nombre de répétitions
        if random()<p :
            c = c + 1 # ou c += 1
    return c  # ou c/n pour être en fréquence


    
###### programme de simulation #########
def jeu(taille, nb_echantillon):
    p = 0.1+0.8*random()    # proportion dans la population aléatoire entre 0,1 et 0,9
#    n = 10                  # n est la taille des échantillons
 #   nb_echantillon = 100    # le nombre d'échantillons simulés 
    print("Taille d'échantillon :", taille)
    print("Nombre d'échantillons :", nb_echantillon)
    for i in range(1,nb_echantillon+1):
        freq = nb_succes(taille, p)/taille # calcul de la fréquence
        plt.plot(i, freq,'b+')  # représenté en bleu par une croix

    # représentation graphique

    plt.axis([0,100,0,1])
    plt.grid(True)
    plt.xlabel('Echantillon n°')
    plt.ylabel("Fréquence dans l'échantillon")
    plt.show()

    reponse=float(input("proposer une valeur de la proportion p dans la population: "))

    if p==reponse:
        print("Parfait, c'est la bonne estimation, bravo !")
    else:
        if abs(p-reponse) < 0.0501:
            print("C'est une bonne estimation ! La vraie valeur de p est", round(p,5) ,"\n l'écart n'est donc que de",round(abs(p-reponse),3),"avec votre réponse.")
        else :
            print("C'est une estimation assez imprécise ! La vraie valeur de p était",p)

jeu(10, 100)

Je ne suis pas certain que ce soit très efficace pour que les élèves se rendent compte qu'un échantillon ne fournit pas précisément la proportion inconnue dans une population.

Observer la loi des grands nombres à l’aide d’une simulation sur Python ou tableur.¶

La fréquence de succès d’un événement sur un échantillon s’approche de la probabilité de cet événement sur la population lorsque sa taille augmente.

Illustrons cela avec un jeu de dé :

On lance un dé à 6 faces non truqué.
- Si c’est 1 qui sort, on gagne 1€.
- Si c’est 2, 3 ou 4 qui sort, on gagne 2€.
- Sinon, on gagne 4€.

L’espérance de gain à ce jeu est donc $\dfrac{1 \times 1 + 3 \times 2 + 2 \times 4}{6}=2,5$ €.

On définit la fonction jeu() dans un premier temps :

from random import randint

def jeu():
    de = randint(1,6)       # on tire au hasard un nombre entier parmi 1, 2, 3, 4, 5 et 6.
    if de < 2:
        return 1
    elif de < 5:
        return 2
    else:
        return 4

Puis une représentation graphique d'un nombre donné de répétitions :

import matplotlib.pyplot as plt  # import du traitement grahique

def evolutionMoyenne(n_repetition):
    s = 0  # on n'a encore rien gagné
    L = [] # on créé une liste vide
    for n in range(n_repetition):
        s = s + jeu() # s est le gain cumulé
        L.append(s/(n+1)) # On ajoute la moyenne des n+1 répétitions car n varie de 0 à n-1
    plt.plot(list(range(1, n_repetition+1)), L, 'b.')
    plt.plot([1, n_repetition], [2.5, 2.5], 'r-')  #2.5 est l'espérance de gain
    plt.grid()
    plt.show()

evolutionMoyenne(75)

Pour "visualiser" l'intervalle de fluctuation du gain, il peut être intéressant de répéter plusieurs fois l'expérience sur le même dessin.

def evolutionMoyenne_(n_repetition):
    for i in range(10):
        s = 0  # on n'a encore rien gagné
        L = [] # on créé une liste vide
        for n in range(n_repetition):
            s = s + jeu() # s est le gain cumulé
            L.append(s/(n+1)) # On ajoute la moyenne des n+1 répétitions car n varie de 0 à n-1
        plt.plot(list(range(1, n_repetition+1)), L, 'b.')
        plt.plot([1, n_repetition], [2.5, 2.5], 'r-')  #2.5 est l'espérance de gain
    plt.ylim(2.4, 2.6)
    plt.grid()
    plt.show()

evolutionMoyenne_(10000)